Central composite design

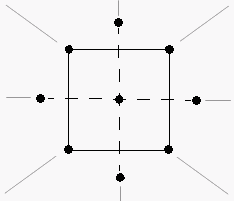
The most commonly used response surface experimental design. Central composite designs consist of a factorial or fractional factorial design with center points, augmented with a group of axial (or star) points that allow estimation of curvature. You can use a central composite design to:

·    Efficiently estimate first- and second-order terms

·    Model a response variable with curvature by adding center and axial points to a previously-run factorial design.

Central composite designs are especially useful in sequential experiments because you can often build on previous factorial experiments by adding axial and center points.

For example, you would like to determine the best conditions for injection-molding a plastic part. You first run a factorial experiment and determine  the significant factors: temperature (levels set at 190° and 210°) and pressure (levels set at 50MPa and 100MPa).  You can use a response surface designed experiment to find the optimal settings for each factor. Here are the design points for this experiment:

(Design center point is 200°, 75MPa)

When possible, central composite design have the desirable properties of orthogonal blocking and rotatability.

·    Orthogonal blocking – Often, central composite designs are run in more than one block. Central composite designs can  block orthogonally, allowing for model terms and block effects to be estimated independently and minimizing the variation in the regression coefficients.

·    Rotatability – Rotatable designs provide the desirable property of constant prediction variance at all points that are equidistant from the design center.

Face centered designs are a type of central composite design with an alpha of 1. In this design the axial points or "star" points are at the center of each face of the factorial space, so levels = + 1. This variety of design requires 3 levels of each factor. Augmenting an existing factorial or resolution V design with appropriate star points can also produce this design.