Example of Regression with Life Data
main topic     interpreting results     session command     see also 

Suppose you want to investigate the deterioration of an insulation used for electric motors. You want to know if you can predict failure times for the insulation based on the plant in which it was manufactured, and the temperature at which the motor runs. It is known that an Arrhenius relationship exists between temperature and loge failure time.

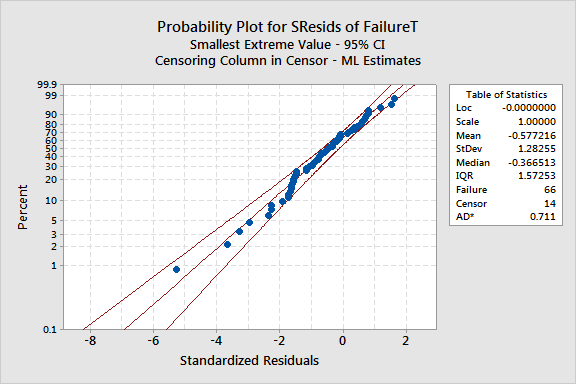
You gather failure times at plant 1 and plant 2 for the insulation at four temperatures - 110, 130, 150, and 170° C. Because the motors generally run at between 80 and 100° C, you want to predict the insulation's behavior at those temperatures.

To see how well the model fits, you will draw a probability plot based on the standardized residuals.

1    Open the worksheet INSULATE.MTW.

2    Choose Stat > Reliability/Survival > Regression with Life Data.

3    In Variables/Start variables, enter FailureT.

4    In Model, enter ArrTemp Plant. In Factors (optional), enter Plant.

5    Click Censor. In Use censoring columns, enter Censor, then click OK.

6    Click Estimate. In Enter new predictor values, enter ArrNewT NewPlant, then click OK.

7    Click Graphs. Check Probability plot for standardized residuals, then click OK in each dialog box.

Session window output

Regression with Life Data: FailureT versus ArrTemp, Plant

 

 

Response Variable: FailureT

 

Censoring Information  Count

Uncensored value          66

Right censored value      14

 

Censoring value: Censor = C

 

Estimation Method: Maximum Likelihood

 

Distribution:   Weibull

 

Relationship with accelerating variable(s):   Linear

 

 

Regression Table

 

                       Standard                    95.0% Normal CI

Predictor       Coef      Error       Z      P      Lower       Upper

Intercept   -15.3411   0.950822  -16.13  0.000   -17.2047    -13.4775

ArrTemp     0.839255  0.0339710   24.71  0.000   0.772673    0.905837

Plant

 2         -0.180767  0.0845721   -2.14  0.033  -0.346525  -0.0150083

Shape        2.94309   0.270658                   2.45768     3.52439

 

Log-Likelihood = -562.525

 

 

Table of Percentiles

 

                                     Standard   95.0% Normal CI

Percent  ArrTemp  Plant  Percentile     Error    Lower    Upper

     50  32.8600      1      182094   32466.2   128390   258261

     50  32.8600      2      151981   25286.6   109690   210578

     50  31.0988      1     41530.4   5163.76  32548.4  52990.9

     50  31.0988      2     34662.5   3913.87  27781.0  43248.6

Graph window output:

 

Interpreting the results

From the Regression Table, you get the coefficients for the regression model. For the Weibull distribution, here is the equation that describes the relationship between temperature and failure time for the insulation for plant 1 and 2, respectively:

Loge (failure time) = -15.3411 + 0.83925 (ArrTemp) + 1/2.9431

Loge (failure time) = -15.52187 + 0.83925 (ArrTemp) + 1/2.9431

where = the pth percentile of the error distribution

ArrTemp = 11604.83/(Temp + 273.16)

The Table of Percentiles displays the 50th percentiles for the combinations of temperatures and plants that you entered. The 50th percentile is a good estimate of how long the insulation will last in the field:

·    For motors running at 80° C, insulation from plant 1 lasts about 182093.6 hours or 20.77 years; insulation from plant 2 lasts about 151980.8 hours or 17.34 years.

·    For motors running at 100° C, insulation from plant 1 lasts about 41530.38 hours or 4.74 years; insulation from plant 2 lasts about 34662.51 hours or 3.95 years.

As you can see from the low p-values, the plants are significantly different at the a = .05 level, and temperature is a significant predictor.

The probability plot for standardized residuals will help you determine whether the distribution, transformation, and equal shape (Weibull or exponential) or scale parameter (other distributions) assumption is appropriate. Here, the plot points fit the fitted line adequately; therefore you can assume the model is appropriate.