Outlier

An unusually large or small observation.  Outliers can have a disproportionate influence on statistical results, such as the mean, which can result in misleading interpretations. For example, a data set includes the values: 1, 2, 3, and 34. The mean value, 10, which is higher than the majority of the data (1, 2, 3), is greatly influenced by the extreme data point, 34. In this case, the mean value makes it appear that the data values are higher than they really are. You should investigate outliers because they can provide useful information about your data or process. Several explanations for outliers exist:

·    Data-entry error: Correct the error and reanalyze the data

·    Process issue: Investigate the process to determine the cause of the outlier

·    Missing factor: Determine whether you failed to account for a factor that influences the process

·    Random chance: Investigate the process and the outlier to determine if it occurred by chance; perform the analysis with and without the outlier to see its impact on the results

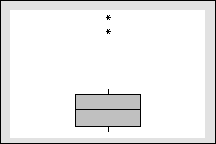
Often, it is easiest to identify outliers graphically. Minitab identifies outliers on boxplots by labeling observations that are at least 1.5 times the interquartile range (Q3 – Q1) from the edge of the box. For example, a company tracks late payments based on number of days past due. The boxplot below shows two outliers, indicating two accounts that are extremely overdue. An analyst researches the accounts and discovers that the customers moved and never received their bills.

Boxplot

In model-fitting procedures such as regression and ANOVA, outliers are points that are not explained well by the fitted model. These points are outlying in the y-direction relative to the fitted regression line and have extreme residual values. Minitab labels observations with extreme residual values (+ 2) with an R in the table of unusual observations. You can also identify these outliers graphically, using scatterplots and residual plots, as shown below.

Scatterplot

Use diagnostic measures, such as Cook's distance or DFITS to determine whether the outlier is an influential observation. To determine the effect of the outlier on your results, run the analysis with and without the observation to see how the model changes. Note that an observation may be an outlier in one model but not in another. For example, an observation may be an outlier in a linear model but it is well-explained by a nonlinear model.