Mean cumulative function and Nelson-Aalen plot

The mean cumulative function is the average cumulative number of failures or cost over all systems in the time interval (0, t). This function is overlaid on the Nelson-Aalen plot to help you determine how the number of failures or your repair costs are changing over time. In other words, it describes your system as improving, deteriorating, or staying constant.

The overlaid plot consists of:

·    The Nelson-Aalen plot, which is a plot of the empirical mean cumulative function. The plot points do not assume a particular model. When you have interval data, Minitab estimates failure times by evenly distributing the number of occurrences in each interval and plotting the appropriate points.

·    The mean cumulative function curve, which is a plot of the mean cumulative function based on the estimated shape and scale. The function appears as a straight line or a curve. For a power-law process, the rate of system failures can increase, decrease, or remain constant. For a homogeneous Poisson process, the failure rate is constant, resulting in a straight line.

Because the Nelson-Aalen plot does not depend on the model, the plot points are the same regardless of which estimation method and model type you chose. The mean cumulative function plot, however, differs depending on your model.

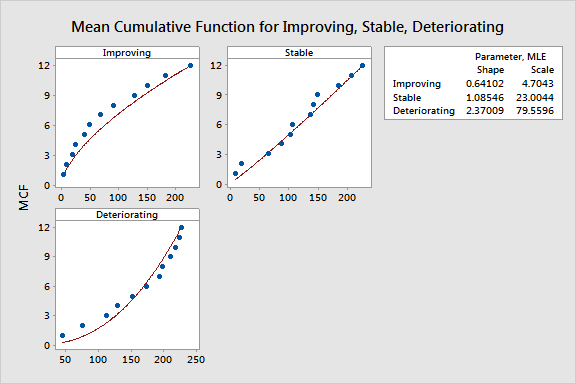
The plot provides information about the pattern of system failures:

·    A straight line pattern indicates that system failures are remaining constant over time - your system is stable

·    A convex (curving down) pattern indicates that the time between failures is increasing over time - your system reliability is improving

·    A concave (curving up) pattern indicates that the time between failures is decreasing over time - your system reliability is deteriorating

Below are examples of mean cumulative function and Nelson-Aalen plots for improving, stable, and deteriorating systems.