
Generates an equation to describe the nonlinear relationship between a continuous response variable and one or more predictor variables, and predicts new observations. Use nonlinear regression instead of ordinary least squares regression when you cannot adequately model the relationship with linear parameters. Parameters are linear when each term in the model is additive and contains only one parameter that multiplies the term.
You must specify the expectation function that Minitab uses to perform nonlinear regression. Your choice for the function often depends on prior knowledge about the response curve's shape or the behavior of physical and chemical properties in the system. Potential nonlinear shapes include concave, convex, exponential growth or decay, sigmoidal (S), and asymptotic curves. In either case, you need to specify the function that satisfies both the requirements of your prior knowledge and the nonlinear regression assumptions.
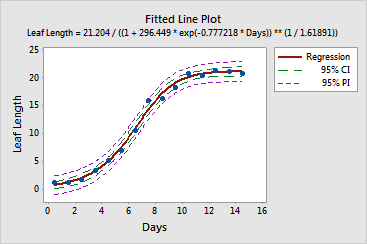
For example, researchers study the growth rate of leaves. They measure leaf lengths at different points in time. Based on their research, they decide to use the Richards growth model, a sigmoidal function that is often used in botany. Among other output, the Nonlinear Regression command produces this fitted line plot that displays the relationship and regression equation.
