Original
Log10 Transform
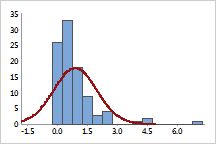
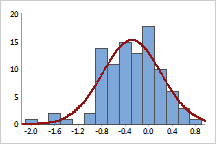
The data are positively skewed, as shown by the values far out on the right (upper) tail.
The log10 transformation compresses the upper tail and stretches out the lower tail, making the data appear more normal.

The exponent to which 10 must be raised to equal a given number. For example, 102 = 100, so the log base 10 of 100 is 2. Log base 10 is defined only for positive numbers. When you multiply a number by 10, you increase its log by 1; when you divide a number by 10, you decrease its log by 1.
In statistics, log base 10 (log10) can be used to transform data for the following reasons:
|
Original |
|
Log10 Transform |
|
|
|
|
|
The data are positively skewed, as shown by the values far out on the right (upper) tail. |
|
The log10 transformation compresses the upper tail and stretches out the lower tail, making the data appear more normal. |
|
Original |
|
Log10 Transform |
|
|
|
|
|
The simple regression line does not accurately model the curvature in the data on the scatterplot. |
|
After the X-scale is transformed using log10, the data values fall along the simple regression line. |
|
Original |
|
Log10 Transform |
|
|
|
|
|
Group 1 has larger values and thus appears to have greater within-group variability. |
|
After the data are transformed, the within-group variation appears similar. |
In Minitab, you can use Regression > Fitted Line Plot > Options to transform response or predictor variables using log10, if the regression model contains only nonnegative data. You can also use log10 to transform scales for scatterplots, time series plots, and area graphs.
To find the log base 10 of a number or column of numbers, use the Calculator. If you calculate log base 10 of zero or a negative number, Minitab stores a missing value (*).