|
|
Line Plot |
Line plots typically contain the following elements:
Line plots are particularly helpful for identifying relationships between two factors and the response. To identify possible relationships, look for the following:
Example Output |
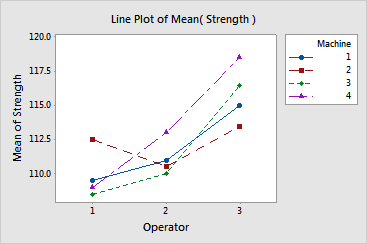
Interpretation |
|
For the textile strength data, the non-zero slope of all lines suggests differences in the mean strength between operators. Operator 1 generally produced the lowest mean strength regardless of the machine used, while operator 3 produced the highest mean strength.
On the other hand, the effect of machine is not consistent. Any given machine produces a high or low mean strength depending on the operator. The non-parallel line associated with operator 1 on machine 2 suggests a possible interaction. This combination produced an unexpectedly high mean strength that may warrant a follow-up investigation.
Overall, operator appears to be a strong factor in textile strength. The machine's effect on strength is less pronounced and possibly statistically insignificant. Additionally, there may be an interaction effect. To determine if these effects are statistically significant, conduct an appropriate test such as an ANOVA.