|
|
Comparisons (GLM)Multiple Comparisons |
Use the confidence intervals generated by the Fisher method to determine whether two means are different:
The individual confidence level indicates the percentage of times that a confidence interval contains the true difference for one comparison if the study were repeated multiple times.
For the Fisher method, examine the simultaneous confidence level because it can decrease to an unacceptable level. To display the simultaneous confidence level and the values of the confidence limits in the Session window, check Tests and confidence intervals in Stat > ANOVA > General Linear Model > Comparisons > Results.
Example Output |
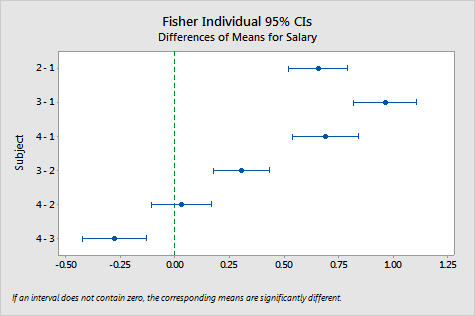
Interpretation |
For the salary analysis, all pairwise comparisons were requested for the subject factor. The confidence level chosen for the intervals was 95%, which corresponds to an individual error rate of 0.05 (or 5%). Because there are four levels of subject, this produces six pairwise comparisons. The confidence intervals for the comparisons reveal the following:
The hypothesis test table indicates that the simultaneous confidence level for this family of comparisons is 80.38%. We can be 80.38% confident that all of these confidence intervals contain the true differences.