Example of Capability Analysis for Multiple Variables
(Normal)main topic interpreting results session command see also
Example of Capability Analysis for Multiple Variables
(Normal)Suppose you are interested in the capability of a process that produces support beams. You are concerned that the thickness of the beam might be affected by the morning and evening shift. You measure the thickness of 5 samples out of 10 boxes produced in each shift. The thickness must be between 10.44 mm and 10.96 mm to meet the requirement.
1 Open the worksheet MCAPA.MTW.
2 Choose Stat > Quality Tools > Capability Analysis > Multiple Variables (Normal).
3 In Variables, enter Thickness. In Subgroup sizes, enter 5.
4 Check By variables, enter Shift.
5 In Lower spec, enter 10.44. In Upper spec, enter 10.96.
6 Click OK.
Session window output
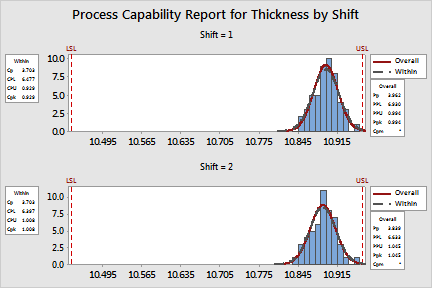
Process Capability Report for Thickness by Shift
Process Data
Shift LSL Target USL Sample Mean Sample N StDev(Within) 1 10.44 * 10.96 10.8948 50 0.0234052 2 10.44 * 10.96 10.8892 50 0.0234052
Shift StDev(Overall) 1 0.0218753 2 0.0225732
Overall Capability
Shift Pp PPL PPU Ppk Cpm 1 3.962 6.930 0.994 0.994 * 2 3.839 6.633 1.045 1.045 *
Potential (Within) Capability
Shift Cp CPL CPU Cpk 1 3.703 6.477 0.929 0.929 2 3.703 6.397 1.008 1.008
Observed Performance
Shift PPM < LSL PPM > USL PPM Total 1 0.00 0.00 0.00 2 0.00 0.00 0.00
Exp. Within Performance
Shift PPM < LSL PPM > USL PPM Total 1 0.00 2670.58 2670.58 2 0.00 1243.30 1243.30
Exp. Overall Performance
Shift PPM < LSL PPM > USL PPM Total 1 0.00 1438.77 1438.77 2 0.00 855.01 855.01 |
Graph window output
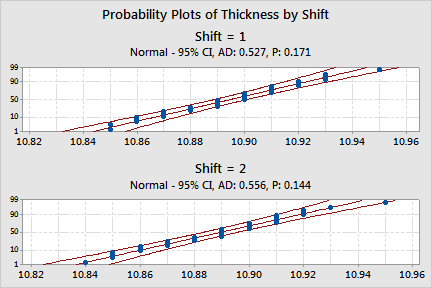
If you want to interpret the process capability statistics, your data should approximately follow a normal distribution. This requirement appears to have been fulfilled, as shown by the probability plot.
Cp is defined as the ratio of the specification range to the potential process range ( the 6-swithin variation). Cp = 3.703 for both the shifts indicating that the specification spread for both the shifts is 3.703 times greater than the process range.
CPL and CPU relates the process variation (swithin) and mean (m) to the specification limits. CPL is the ratio of m-LSL to 3-swithin variation. CPU is the ratio of USL-m to swithin variation. The CPL and CPU for both the shifts are not equal, indicating that the process is not centered at the specification midpoint. This is also evident in the histograms.
Cpk is the minimum of CPU and CPL. For both the shifts, high value of Cp and low value of Cpk indicate that the process has a centering problem.
The capability indices in the Overall table measures the actual capability of a process using soverall variation as the process variation. Pp, PPL, PPU, and Ppk are similarly defined as their counterparts in the Within table.
For shift 1, Pp = 3.962 indicate that the specification interval is 3.962 times greater than the process range. For shift 2, Pp = 3.839 indicate that the specification interval is 3.839 times greater than the process range.
PPU and PPL relates the process spread (the 3-soverall variation) to a single-sided specification spread (m-LSL or USL-m). The PPL and PPU for both the shifts indicate that the process is not centered
The potential capability indices are close to the actual indices for both the shifts, which suggests that the variation across subgroup means are small for both shifts.
PPM > USL (2670.58) indicates that 2670 out of 1 million beams exceed the upper specification limit of 10.96 mm.
Industry guidelines determine whether the process is capable. A generally accepted minimum value for the indices is 1.33. For both the shifts, if you ignore the centering problem of the process, the process seems to have high capability. However, if centering of the process is a concern, then you should investigate the issue and improve the process.