Describes the discriminatory power of an acceptance sampling plan. The OC curve plots the probabilities of accepting a lot versus the fraction defective.
|
|
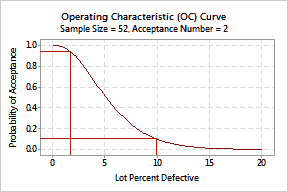
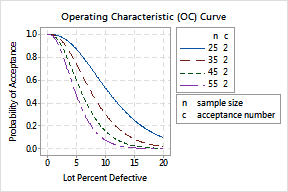
For example, you sample 52 rollers from a shipment of 500. If the actual % defective is 1.5% you have a 0.9567 probability of accepting this lot based on the sample and a 0.0433 probability of rejecting it. If the actual % defective is 10%, you have a 0.0966 probability of accepting this lot and a 0.9034 probability of rejecting it. By plotting the OC curve, the sampling risks are evident. You should always examine the OC curve before adopting a sampling plan. |
You can also compare OC curves to help choose the appropriate sampling plan.
|
|
In this case, the shift supervisor thinks sampling 52 rollers from 500 is too much. You can develop curves for various sample sizes and acceptance numbers to illustrate the increased risk. If the sample size is 35 (red line) and the % defective is 10%, you now have a 0.306 probability of accepting this lot. |
Look at OC curves, AOQ curves, and ATI curves together when evaluating sampling plans.
| Minitab help | Stat | Graph | SixSigma | DOE | Glossary | Reliability | SPC,MSA,CPK | ||
|
|||||||||
