Example of a Distribution ID Plot for right-censored data
main topic     interpreting results     session command     see also 

Suppose you work for a company that manufactures engine windings for turbine assemblies. Engine windings may decompose at an unacceptable rate at high temperatures. You want to know - at given high temperatures - the time at which 1% of the engine windings fail. You plan to get this information by using Parametric Distribution Analysis (Right Censoring), which requires you to specify the distribution for your data. Distribution ID Plot - Right Censoring can help you choose that distribution.

First you collect failure times for the engine windings at two temperatures. In the first sample, you test 50 windings at 80° C; in the second sample, you test 40 windings at 100° C. Some of the units drop out of the test for unrelated reasons. In the Minitab worksheet, you use a column of censoring indicators to designate which times are actual failures (1) and which are censored units removed from the test before failure (0).

1    Open the worksheet RELIABLE.MTW.

2    Choose Stat > Reliability/Survival > Distribution Analysis (Right Censoring) > Distribution ID Plot.

3    In Variables, enter Temp80 Temp100.

4    Choose Specify. Leave the default distributions as Weibull, lognormal, exponential, and normal.

5    Click Censor. Choose Use censoring columns and enter Cens80 Cens100 in the box. Click OK in each dialog box.

Session window output

Distribution ID Plot:  Temp80, Temp100

 

 

Results for variable: Temp80

 

 

Goodness-of-Fit

 

              Anderson-Darling

Distribution             (adj)

Weibull                 68.204

Lognormal               67.800

Exponential             70.871

Normal                  68.305

 

 

Table of Percentiles

 

                                   Standard    95% Normal CI

Distribution  Percent  Percentile     Error     Lower    Upper

Weibull             1     10.0765   2.78453   5.86263  17.3193

Lognormal           1     19.3281   2.83750   14.4953  25.7722

Exponential         1    0.809731  0.133119  0.586684  1.11758

Normal              1   -0.549323   8.37183  -16.9578  15.8592

 

Weibull             5     20.3592   3.79130   14.1335  29.3273

Lognormal           5     26.9212   3.02621   21.5978  33.5566

Exponential         5     4.13258  0.679391   2.99422  5.70371

Normal              5     18.2289   6.40367   5.67790  30.7798

 

Weibull            10     27.7750   4.11994   20.7680  37.1463

Lognormal          10     32.1225   3.09409   26.5962  38.7970

Exponential        10     8.48864   1.39552   6.15037  11.7159

Normal             10     28.2394   5.48103   17.4968  38.9820

 

Weibull            50     62.6158   4.62515   54.1763  72.3700

Lognormal          50     59.8995   4.31085   52.0192  68.9735

Exponential        50     55.8452   9.18089   40.4622  77.0766

Normal             50     63.5518   4.06944   55.5759  71.5278

 

 

Table of MTTF

 

                       Standard    95% Normal CI

Distribution     Mean     Error    Lower    Upper

Weibull       64.9829    4.6102  56.5472   74.677

Lognormal     67.4153    5.5525  57.3656   79.225

Exponential   80.5676   13.2452  58.3746  111.198

Normal        63.5518    4.0694  55.5759   71.528

 

 

Results for variable: Temp100

 

 

Goodness-of-Fit

 

              Anderson-Darling

Distribution             (adj)

Weibull                 17.339

Lognormal               17.253

Exponential             18.879

Normal                  17.781

 

 

Table of Percentiles

 

                                    Standard     95% Normal CI

Distribution  Percent  Percentile      Error     Lower     Upper

Weibull             1     2.98186    1.26067   1.30201   6.82903

Lognormal           1     6.87764    1.61698   4.33827   10.9034

Exponential         1    0.502517  0.0861809  0.359063  0.703284

Normal              1    -18.8392    8.80960  -36.1057  -1.57266

 

Weibull             5     8.17115    2.36772   4.63056   14.4189

Lognormal           5     11.3181    2.07658   7.89954   16.2162

Exponential         5     2.56466   0.439836   1.83253   3.58931

Normal              5   -0.298373    6.86755  -13.7585   13.1618

 

Weibull            10     12.7534    2.97772   8.07016   20.1543

Lognormal          10     14.7606    2.35025   10.8036   20.1667

Exponential        10     5.26803   0.903459   3.76416   7.37272

Normal             10     9.58565    5.95326  -2.08252   21.2538

 

Weibull            50     40.8900    4.73799   32.5827   51.3153

Lognormal          50     37.6636    4.43620   29.8995   47.4439

Exponential        50     34.6574    5.94369   24.7637   48.5038

Normal             50     44.4516    4.37371   35.8793   53.0240

 

 

Table of MTTF

 

                       Standard    95% Normal CI

Distribution     Mean     Error    Lower    Upper

Weibull       45.9448   4.87525  37.3177  56.5663

Lognormal     49.1969   6.91761  37.3465  64.8076

Exponential   50.0000   8.57493  35.7265  69.9761

Normal        44.4516   4.37371  35.8793  53.0240

 

 

Distribution ID Plot for Temp80, Temp100

Graph window output

 

Interpreting the results

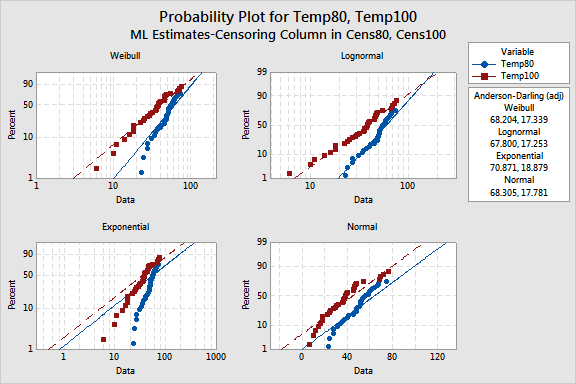
The points fall approximately on the straight line on the lognormal probability plot, so the lognormal distribution would be a good choice when running the parametric distribution analysis. You can also compare the Anderson-Darling goodness-of-fit values to determine which distribution best fits the data. A smaller Anderson-Darling statistic means that the distribution provides a better fit. Here, the Anderson-Darling values for the lognormal distribution are lower than the Anderson-Darling values for other distributions, thus supporting your conclusion that the lognormal distribution provides the best fit.

The table of percentiles and MTTFs allow you to see how your conclusions may change with different distributions.

 

Minitab help Stat Graph SixSigma DOE Glossary Reliability SPC,MSA,CPK
Create Pareto chart - Free tool

Calendar with week numbers

US Federal Holidays

Australia Public Holidays