|
|
One-Way ANOVAGraphs - Hsu Simultaneous CIs |
Hsu's method compares the mean of each factor level with the best remaining factor level mean. You must specify whether the smallest or the largest mean is considered best.
This method uses a family error rate (often called familywise error rate) to control the rate of type I error. The family error rate is the probability of making one or more type I errors for the entire set of comparisons. This rate must be set before using the method.
Results are presented as a set of simultaneous confidence intervals for the difference between pairs of means. No grouping information table is presented for Hsu's MCB.
Use the confidence intervals to determine likely ranges for the differences and to assess the practical significance of the differences.
To display the values of the confidence limits in the Session window, check Tests in Stat > ANOVA > One-Way > Comparisons.
Example Output |
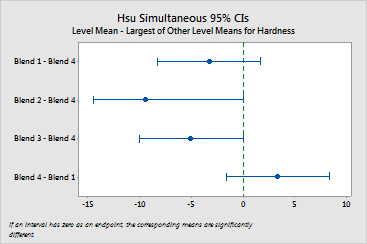
Interpretation |
For the paint hardness analysis, the largest mean was specified as the best. Therefore, the means for Blend 1 (14.733), Blend 2 (8.567), and Blend 3 (12.983) are all compared to the mean for Blend 4 (18.067) because this is the largest (best) mean. The mean for Blend 4 itself is compared to the mean of Blend 1, because this is the largest of the remaining three means.
The results indicate the following: