|
|
One-Way ANOVAGraphs - Games-Howell CIs for Differences of Means |
The Games-Howell method compares the means for each pair of factor levels using a family error rate (often called familywise error rate) to control the rate of type I error. The family error rate is the probability of making one or more type I errors for the entire set of comparisons. The Games-Howell method adjusts the individual confidence level, based on the family error rate you choose.
This method is only available if you do not assume that all populations have equal variances.
Use the confidence intervals to determine likely ranges for the differences and to assess the practical significance of the differences.
To display the values of the confidence limits in the Session window, check Tests in Stat > ANOVA > One-Way > Comparisons.
Example Output |
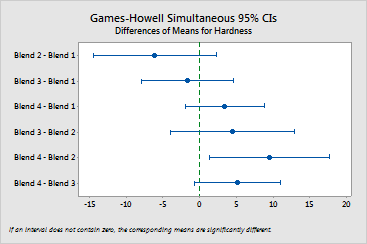
Interpretation |
For the paint hardness data, the confidence intervals display the likely ranges for all the mean differences: