Example of Gage R&R Study (ANOVA method)
main topic     interpreting results     session command     see also 

In this example, we do a gage R&R study on two data sets: one in which measurement system variation contributes little to the overall observed variation (GAGEAIAG.MTW), and one in which measurement system variation contributes a lot to the overall observed variation (GAGE2.MTW). For comparison, we analyze the data using both the ANOVA method (below) and the Xbar and R method. You can also look at the same data plotted on a Gage Run Chart.

The GAGEAIAG data was taken from Measurement Systems Analysis Reference Manual, 3rd edition. (Chrysler, Ford, General Motors Supplier Quality Requirements Task Force). Ten parts were selected that represent the expected range of the process variation. Three operators measured the ten parts, three times per part, in a random order.

For the GAGE2 data, three parts were selected that represent the expected range of the process variation. Three operators measured the three parts, three times per part, in a random order.

Step 1: Use the ANOVA method with GAGEAIAG data

1    Open the worksheet GAGEAIAG.MTW.

2    Choose Stat > Quality Tools > Gage Study > Gage R&R Study (Crossed).

3    In Part numbers, enter Part.

4    In Operators, enter Operator.

5    In Measurement data, enter Measurement.

6    Under Method of Analysis, choose ANOVA.

7    Click Options. Under Process tolerance, choose Upper spec - Lower spec and enter 8.

8    Click OK in each dialog box.

Step 2: Use the ANOVA method with GAGE2 data

1    Open the file GAGE2.MTW.

2    Choose Stat > Quality Tools > Gage Study > Gage R&R Study (Crossed).

3    In Part numbers, enter Part.

4    In Operators, enter Operator.

5    In Measurement data, enter Response.

6    Under Method of Analysis, choose ANOVA.

7    Click OK.

Session window output

ANOVA method with GAGEAIAG data

ANOVA method with GAGE2 data

Graph window output

ANOVA method with GAGEAIAG data

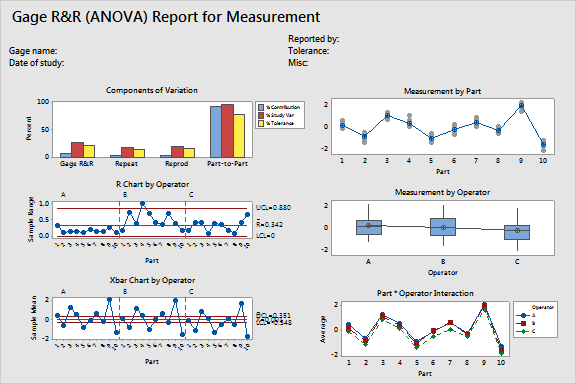
ANOVA method with GAGE2 data

Interpreting the results

Session Window Output - GAGEAIAG.MTW

·    Look at the p-value for the Operator*Part interaction in the ANOVA Table. When the p-value for Operator by Part is > 0.05, Minitab omits this from the full model. Notice there is an ANOVA table without the interaction because the p-value was 0.974.

·    Look at the %Contribution column in the Gage R&R table - the percent contribution from Part-To-Part (92.24) is larger than that of Total Gage R&R (7.76). This tells you that much of the variation is due to differences between parts.

·    Look at the %Study Var column - the Total Gage R&R equals 27.86% of the study variation. While the Total Gage R&R %Contribution is acceptable, there is room for improvement. See Guidelines for measurement system acceptability.

·    For this data, the number of distinct categories is four. According to the AIAG, you need at least five distinct categories to have an adequate measuring system. See Number of distinct categories statement.

Graph Window Output - GAGEAIAG.MTW

·    In the Components of Variation graph (located in the upper left corner), the percent contribution from Part-To-Part is larger than that of Total Gage R&R, telling you that much of the variation is due to differences between parts.

·    In the By Part graph (located in upper right corner), there are large differences between parts, as shown by the non-level line.

·    In the R Chart by Operator (located in middle of the left corner), Operator B measures parts inconsistently.

·    In the By Operator graph (located in the middle of the right column), the differences between operators are small compared to the differences between parts, but are significant (p-value = 0.00). Operator C appears to measure slightly lower than the others.

·    In the Xbar Chart by Operator (located in lower left corner), most of the points in the X and R chart are outside the control limits, indicating variation is mainly due to differences between parts.

·    The Operator* Part Interaction graph is a visualization of the p-value for Oper*Part - 0.974 in this case - indicating no significant interaction between each Part and Operator.

Session Window Output - GAGE2.MTW

·    Look at the p-value for the Operator*Part interaction in the ANOVA Table. When the p-value for Operator by Part is > 0.05, Minitab fits the model without the interaction and uses the reduced model to define the Gage R&R statistics.

·    Look at the %Contribution column in the Gage R&R table - the percent contribution from Total Gage R&R (84.36) is larger than that of Part-To-Part (15.64). Thus, most of the variation arises from the measuring system; very little is due to differences between parts.

·    Look at the %Study Var column - the Total Gage R&R equals 91.85% of the study variation. The measurement system is unacceptable and must be improved. See Guidelines for measurement system acceptability.

·    A 1 tells you the measurement system is poor; it cannot distinguish differences between parts.

Graph Window Output - GAGE2.MTW

·    In the Components of Variation graph (located in the upper left corner), the percent contribution from Total Gage R&R is larger than that of Part-to-Part, telling you that most of the variation is due to the measurement system - primarily repeatability; little is due to differences between parts.

·    In the By Part graph (located in upper right corner), there is little difference between parts, as shown by the nearly level line.

·    In the Xbar Chart by Operator (located in lower left corner), most of the points in the X and R chart are inside the control limits, indicating the observed variation is mainly due to the measurement system.

·    In the By Operator graph (located in the middle of the right column), there are no differences between operators, as shown by the level line.

·    The Operator*Interaction graph is a visualization of the p-value for Oper*Part - 0.484 in this case - indicating the differences between each operator/part combination are insignificant compared to the total amount of variation.